数学基本思想在小学分数教学中的渗透应用

罗 静 南 婉 维

【摘要】在小学数学教学中如何渗透数学基本思想，帮助积累经验，发展数学思考，首先我在教学中学生通过学习，能够获得适应未来社会生活和进一步发展所必需的重要数学知识以及基本的数学思想方法。在数学领域中数学思想方法不计其数，每一种数学思想方法都闪烁着人类智慧的火花。但小学生的年龄特点决定有些数学思想方法他们不易接受，而且要想把那么多的数学思想方法都渗透给学生也不现实。本文结合教学实际就分数中所用到的数学思想进行探讨，从而为小学生解决有关分数问题提供一些参考。

【关键词】小学分数 数学思想 渗透 应用

分数是小学数学教学的重要内容，是解决问题与分数知识有机结合的数学问题。小学分数教学对于学生数学学习质量有着重要影响，分数学习为学生进一步学习小数与整数打下了坚实基础。在小学数学中,分数充当了小数与整数桥梁的重要作用。在小学阶段，多数小学生对分数应用题产生了困惑，由于分数后面有单位和没有单位所表示的意义不一样，数量关系就比较抽象，题型也复杂多样，学困生学起分数来尤为吃力。因此，教给学生一些基本的数学思想和方法，这样既有益于拓宽学生的思路又能提高学生的解题能力。

1. 数形结合思想的渗透：

著名数学家华罗庚说过:“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休。”这句话形象、简明、扼要地
指出了数和形的相互依赖、相互制约的辩证关系。“数形结合”既
是一种重要的数学思想，也是一种解决数学问题的有效方法。数形结合思想是根据数学问题的题设和结论之间的内在联系，使数量关系和图形巧妙和谐地结合起来，并充分利用这种结合，寻求解题思路，使问题得到解决。将“数”字化为图“形”，或能从“图”形中获取有用的解题“数”字，是数形结合思想的关键所在。例如在教学：一根绳子剪成两段，第一段长 米，第二段是全场的 ，那么两段相比（ B ）

1. 第一段长 B.第二段长 C.两段一样长 D.无法比较

米

第一段就是 第二段是

全长的 全长的

分析：大部分学生都选择了C选项，如果我们用画图法来解决这个问题，就会避免出错，也能很好地让学生理解清楚 米和 之间的区别。

在教学：有两根绳子，第一根长 米，第二根是全场的 ，那么两根相比（ D ）

A第一段长 B.第二段长 C.两段一样长 D.无法比较

画图：

与 米一样长

比 米短

比 米长

分析：大部分学生受上面题的影响都选择了B选项，把两个题目的意思没弄清楚。

2. 对应思想的渗透：
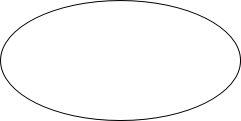
   对应思想在分数应用题中体现得尤为明显。分数应用题的对应主要表现为是“量”与“率”的对应和“图”与“式”的对应等。分数应用题中，每一个数量对于一个确定的标准（单位“1”的量）而言，都有一个对应的分率（即相对数量），每一个分率都对应一个具体的数量。量率对应，寻找对应关系，某种程度上就成了解答分数应用题的关键。教学中通常可以通过“一题多问”、“一题多变”、“一题多解”等方式，促使学生寻找对应关系，渗透对应思想。例如：实验小学举办书法比赛，设一、二、三等奖若干名，其中获一、二等奖的人数占获奖总人数的 ，获二、三等奖的人数占获奖总人数的 。获二等奖的人数占获奖总人数的几分之几？在这个问题中就需要明确单位1（获奖总人数），用单位一来解决问题，我们可以借助集合图来帮助学生理解。

通过图形的帮助，学生很容易理解中间的部分把二等奖获奖人数算了两次（ 里面包含有二等奖人数， 里面也包含有二等奖人数），因此很快列出算式:获二等奖的人数占获奖总人数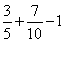

三、归纳思想的渗透：

归纳是一种重要思想，在其指引下可找到对象之间的异同，分析内在关联。在分数授课中如直接告知学生结论，让其死记硬背，不仅容易使其产生枯燥感，还会让学生不求甚解，不利于灵活应用。授课中注重归纳思想的应用，通过给出相关分数或分数运算过程，鼓励其自己动脑思考，总结相关结论，可很好地激发其思考热情给其留下深刻印象。

四、建模思想的渗透：

在《数学课程标准》有这样一句话--“让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感态度与价值观等多方面得到进步和发展”，这实际上就是要求把学生学习数学知识的过程当做建立数学模型的过程并在建模过程中培养学生的数学应用意识,引导学生自觉地
用数学的方法去分析、解决生活中的问题。

数学模型是对某种事物系统的特征或数量依存关系概括或近似表述的数学结构。数学中的各种概念、公式和理论都是由现实世界的原型抽象出来的。狭义地理解,数学模型指那些反映了特定问题或特定具体事物系统的数学关系结构,是相应系统中各变量及其相互关系的数学表达。数学建模就是建立数学模型来解决问题的方法。在小

学阶段,数学模型的表现形式为一系列的概念系统、算法系统、关系、定律、公理系统等。

构建数学模型是引导学生产生知识逻辑性的主要方式。小学分数教学内容本身具有较强的知识连带关系，是除法运算在分数表现形式中的具体呈现。渗透数学基本思想的过程中，教师可以为学生提供相应的分数例题，在例题讲解中引导学生思考分数与除法运算的关系，进而形成更为系统的知识链，加深学生对分数知识体系的总体认知程度。如图中，分数在同一直线内，能否用同一个点来表示?请在图中标注。在运算过程中，教师可提示学生先进行除法运算，由除法运算的结果作为寻找和选择同类型答案的标准。借助线段模型和数据模型，比较最终结构的一致性，最终引导学生在图示线段中标注出具体的点，加深学生对分数意义的理解。通过除法运算模型的构建，引导学生掌握分数运算形式，并总结出数据可能存在的同等关系。

总之，问题是数学的心脏，方法是数学的行为，思想是数学的灵魂。数学思想方法是对数学知识、技能、规律的本质认识，是数学思维的思想结晶，也是解决数学问题的灵魂。数学思想方法可以帮助学生更好地理清思路。在小学数学分数教学中渗透数学基本思想，旨在培养学生的数学思维，加强学生对分数概念、分数运算、分数规律特征的总结。进而加强学生对分数概念及分数算理的理解，增强分数与除法知识点之间的紧密联系，最终培养学生良好的数学思维。

参考文献：

1. 《小学数学经典教学方法》 福建教育出版社 主编：钟建林 方齐珍

2. 《小学数学教学活动设计与案例分析》 科学出版社 主编：李晓梅 孔繁成

3. 苏海滨.浅谈小学高年级分数教学[J].数学学习与研究，2012（16）.