妙用课本例题改编，达成知识结构的重组

甘盈芳

内容摘要：课本例题都是经过专家斟酌而列出的，每道例题往往紧扣本课新内容，对本课内容的运用起到示范引领的作用，然而在具体的教学工作中，我们不仅仅只需要引领学生学会新课内容的运用，还需要对学生前期所学与现在所学间的内在联系进行相互贯通，达成知识结构的重组，提升学生的综合运用的能力．所以为了能在有限的教学时间里达成多维度的教学目标，则要求教师要对课本例题进行阶段性的适度改编，发挥例题教学的最大功能．

关键词：例题，改编，一题多解，结构重组

《义务教育数学课程标准》（2011年版）指出“数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构，是实现数学课程目标，、实施数学教学的重要资源．”．教材的教师用书中的“教学建议”中还提到：“要创造性地使用教材，积极开发、利用各种教学资源，为学生提供丰富的学习素材。”．由此可见，一、教材是实施教学的重要资源；二、教师在使用教材中，不仅要尊重教材，以教材为本，更要发展性地使用教材，创造性地使用教材，这应该成为每个执教者的本能，是教师能力的重要体现．然而，笔者在多年的听课学习中观察到目前仍有相当一部分教师并未能理解教材，领会教材的编者意图，尤其是课本中例题或习题的教学价值的利用情况令人担忧．教师在教学中常受“外来教辅”或教学时间的影响，追求局部的效率，对课本例题使用得不够透彻，从而错失了许多高效的教学机会。下面笔者以人新人教版九年级上册24.1.4圆周角例4的解题教学为例，借此表达对课本例题创造性应用的一些看法．

一、原题展示：

如 图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交于⊙O点D，求BC，AD，BD的长．

课本中的例题解法：

∵AB是⊙O的直径

∴∠ACB=∠ADB=90°

在Rt△ABC中，AB=10cm，AC=6cm

∴AB=

∵CD平分∠ACB

∴∠ACD=∠BCD

∴弧AD=弧BD

∴AD=BD

在Rt△ABD中，

AD=BD=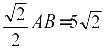 cm

经过深入思考，笔者发现，本例题中有多个常用的“特征条件”，从而使得本题图形在解题中有了多个不同的巧妙的切入点．

特征条件一：直径AB，则图中△ABC与△ABD是两个有公共斜边的直角三角形；

特征条件二：CD是∠ACB的平分线且A、B、C、D四点共圆，则图中有对角互补模型，于是引发思考切入点是否可以将对角互补模型的解题策略用于本题中；

特征条件三：CD平分一个直角且有同弧所对的圆周角，于是图中共有四个45°的角，那么依着45°为切入点可构造45°的直角三角形；

特征条件四：CD平分∠ACB，所得的两个等角在圆中是圆周角，符合圆周角定理的条件，同时符合角平分线的“筝型图”特征．

基于以上的观察与思考，笔者在想，对本题稍作改编，那么就可得到一道可起到圆与多边形问题完美转化，是多种不同的解题切入点和图形模型构造的解题策略对比的载体．用这样的题目为例题可起到事半功倍的奇效．

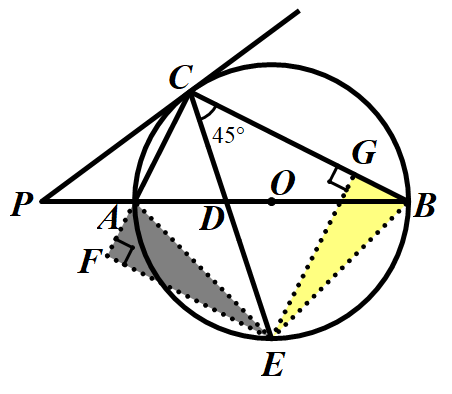
原 题一次改编（用于本章例题学习之后，进一步对例题进行变式使用）：如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交于⊙O点D，求CD的长．

解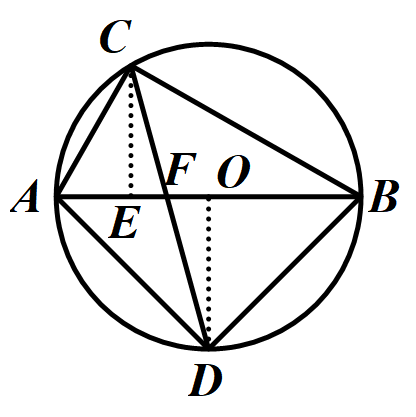 法一：

过点C分别作CE⊥AB，连接DO，可证得DO⊥AB

由等面积法可求得CE=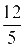 ，DF=5，

再由△ACE∽△ABC求得AE=3.6，所以OE=1.4

证得△FCE∽△FDO，从而求得EF，OF．

再由勾股定理示得CF，DF，进而求得CD的长度

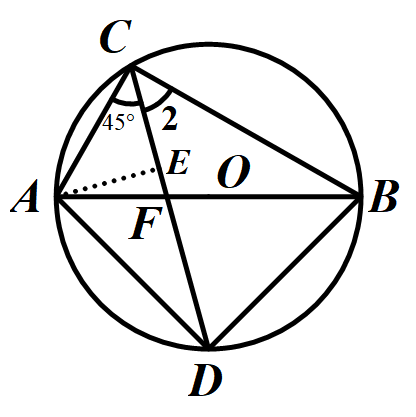
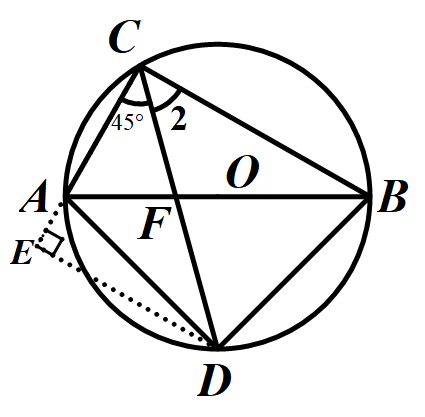
解 法二：联系到特殊角∠ACD=∠BCD=45°，易想到从等腰直角三角形的角度出发作辅助线．

根据45°特殊角联想到等腰直角三角形，从而构造出等腰直角三角形，再经历两次勾股定理，可求出CD的长度．

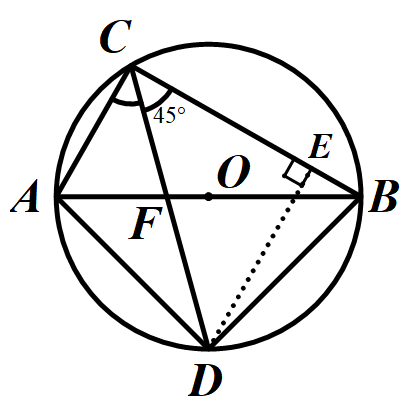
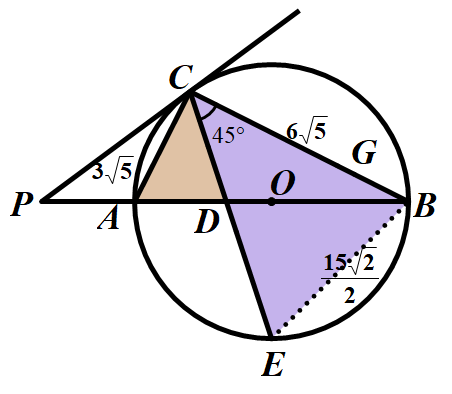
解法三：联系到CD平分∠ACB，易想到从筝形图的角度出发作辅助线，即过点D作DE⊥BC，DG⊥AC．

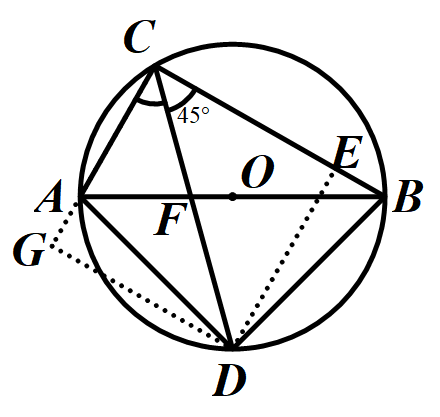
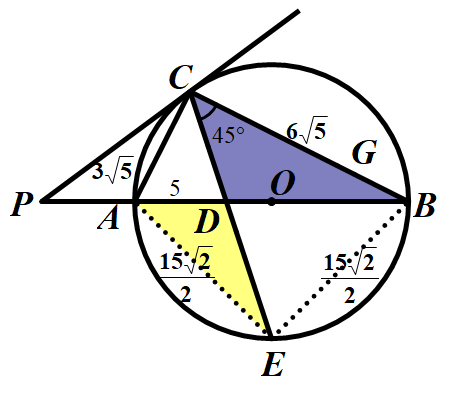
解法四：由四点共圆，联想到对角互模型，从而想到可作如下的辅助线，再借助45°角可得等腰直角三角形．

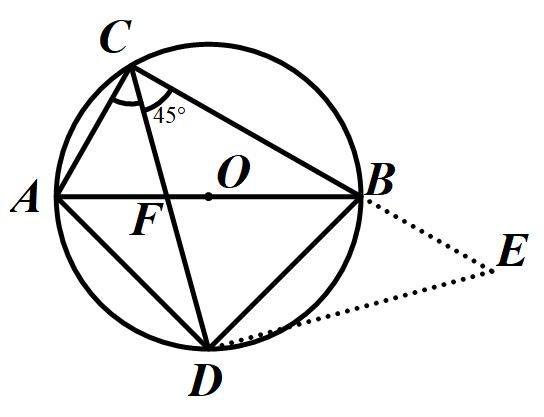
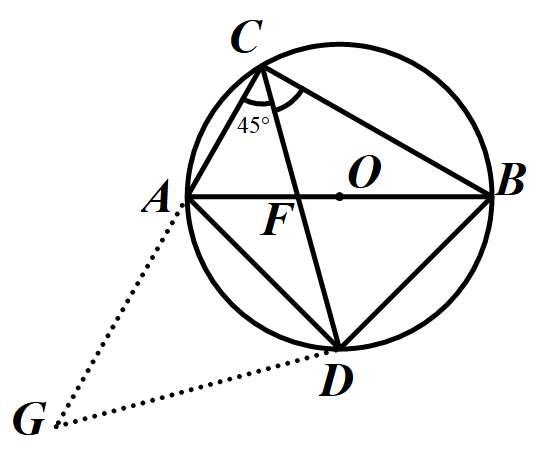
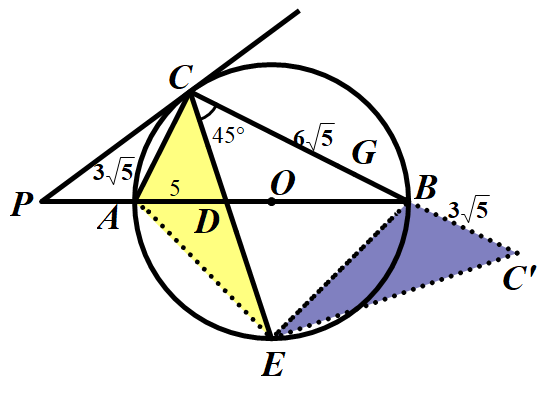
原题二次改编（用于九下学习了相似或锐角三角函数之后）：已知，如图△ABC内接于⊙O，AB是⊙O的直径，过点C做⊙O的切线交BA延长线于P点，点E是弧AB的中点，连接CE交AB于点D，PC=PD.

（1）若PA=5，PC=10，求⊙O的半径r；

（2）在（1）问的条件下，若AC=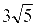 ，求CE的长．

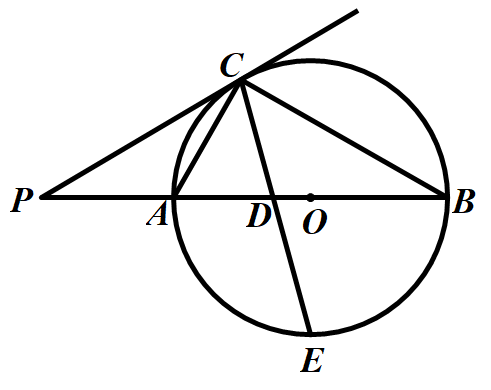
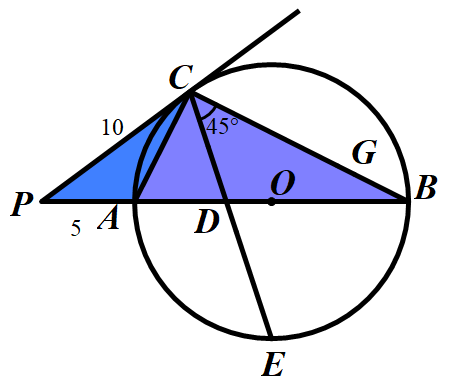
（1）问的解法，证得△PAC∽△PCB，相似比为1:2，即PC ²=PA•PB，求得PB=20，于是AB=15，r =7.5

（2）问的解法展示：

借助45°特殊角构造直角三角形，利用勾股定理、锐角三角函数求长度．

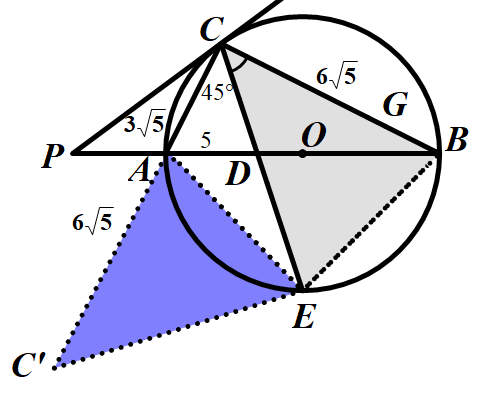
抓住图中的半圆的中点，直径，等腰三角形等特征条件，构造相似三角形（直角三角形），利用相似三角形的性质或是锐角三角函数求得

CD的长度．

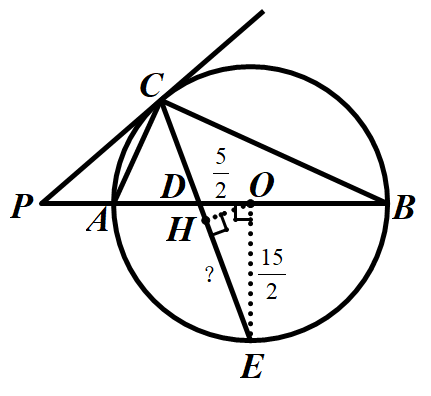
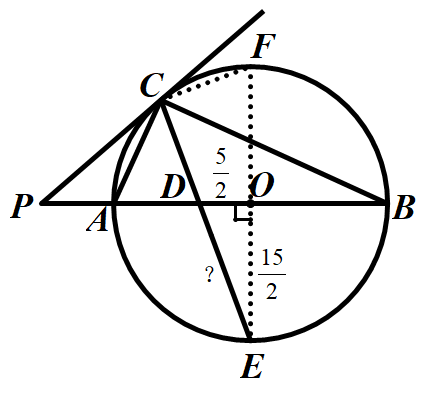
由同弧所对的圆周角相等，构造相似三角形，再利用相似三角形的对应边成比例求长度．

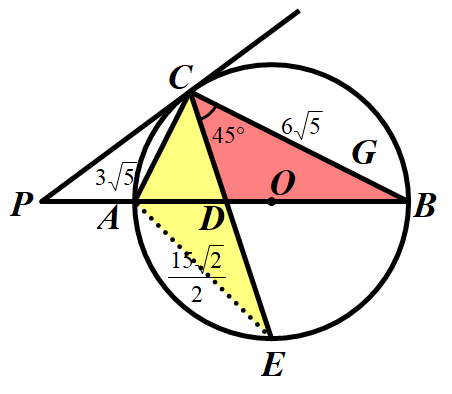
改编思考：

一、通过例题改编，实现多途径解题模式，发挥例题的复习功能．

一般来说，教科书例题是新知识应用的示范引领．教师借助例题，展示如何利用新知识解决问题，并通过例题的示范，使学生学会如何利用新知识分析、解决相关的教学问题．例题大部分致力于“学以致用”，但常规的课堂教学不能只着眼于本节课所学的本身这个点上，而是在以此为基础上以线性发展的眼光，将所学延伸到前期所学内容间的内在联系。本例题原本设定的是针对课本学习内容圆周角定理的应用而为的，所涉及到的知识点和解题方式相对粗浅单薄。然而经过改编后，原本的意图可达成的情况下，还挖掘出了更多的教学价值．尤其是本课设制于九年级的课程，更需要我们有将“新课上出复习课的功能”的观念来指导教学内容设计，在课体例题的基础上，基于不同时期的教学目的进行一次二次改编利用．例题经过改编后，仍旧突出圆的基本性质在解题中应用，实现巩固新知的作用；另一方面又能将由圆的基本性质导出的进一步结论，与多边形（三角形）问题进行串联，从多个不同的角度入手，依据不同的“特征条件”的思考，进行多种不同的图形模型的构造，从而让学生更加深入的体会圆的基本性质对判定多边形的形状或关系起到的特殊的作用和简洁的途径，反过来，特殊多边形（关系）的性质，对求解圆中的几何量起到的重要作用．目的在于，在适当新课教学阶段，适时打通每个新知与旧知间的壁垒，知识结构以网状，面化的形式向前推进，呈现知识与方法的纵横交错关系，同时改变学生对例题过浅，而作业和考试过深，两都间的关联不大的印象．我们要培养学生重视课本例题的良好习惯，因为课本中的例题都是经过专家斟酌而列出的，也是教师与学生日常中接触最多的“教辅”，是教师的“教学”与学生的“学”得以相互成就的主要平台．因此我们在平时的教学和学习中，要认真研读教材，特别是探究例题的解决方法、编者设计意图， 把蕴藏在例题中的问题和隐含的结论挖掘出来．在必要时，我们要对课本例题加以改编，实现例题学习的多维功能化，使学生在学习中得到多维综合运用能力的培养，能对同一问题有不同的观察角度，不同的思维切入点，在解决问题的过程中，体验不同阶段下的知识与方法的综合应用，感悟知识与方法的既交错又统一的关系，在不同的阶段都能实现知识与方法的结构重组。

二、例题教学若辅以思维导图，可突出数学思维过程与方法的提炼，方能起到以一代十的效果．

爱因斯坦曾说：“结论几乎总是以完成的形式出现在读者面前，读者体会不到探索和发现的喜悦，感觉不到思想形成的生动过程，也很难达到清楚地理解全部情况．”这也是数学老师所追求的：把解题方法的形成过程呈现给学生．然而在具体的教学过程中，由于综合题的信息量大，切入点多，分开来看，每一个解法或每一题的解法，学生理解和掌握起来都不困难，但多种不同的解法同时呈现时，则会让学生感到负担重，头脑中往往对本环节中形成的解法感到混乱，最后不知所云，无法达到教师预设的教学效果．在多年的教学实践中，笔者发现，将例题教学以思维导图辅助可以很好地解决这一困境．思维导图作为一种可视化的思考工具，以图形化的方式把题中所给的信息结构化，使其便于更好地分析、理解、联想﹑综合并产生新的想法，使教师从解题过程的解释和阐述中解放出来，着重于引导学生在探究解题思路的过程中主动建构解题思想方法、从而让学生体验到解题的全部过程，达到真正理解．

如第一次改编的教学中，对已知条件进行转化、串联，有目的地筛选、结合，从不同的角度作为切入点，进而引发学生不同的图形构造联想，得到不同的图形模型构造，得到不同的解法．而这些切入点分别体现了圆的哪些性质的使用，在得到这部分“特征条件”后，在多边形状态下，这些“特征条件”又让我们联想到哪些特殊的三角形边形或全等三角形，实现了直线型图形与曲线型图形中的量与量之间的完美互化，使得学生感受解法的自然生成，新知与旧知间的内在联系，积累知识与方法的综合运用的经验．

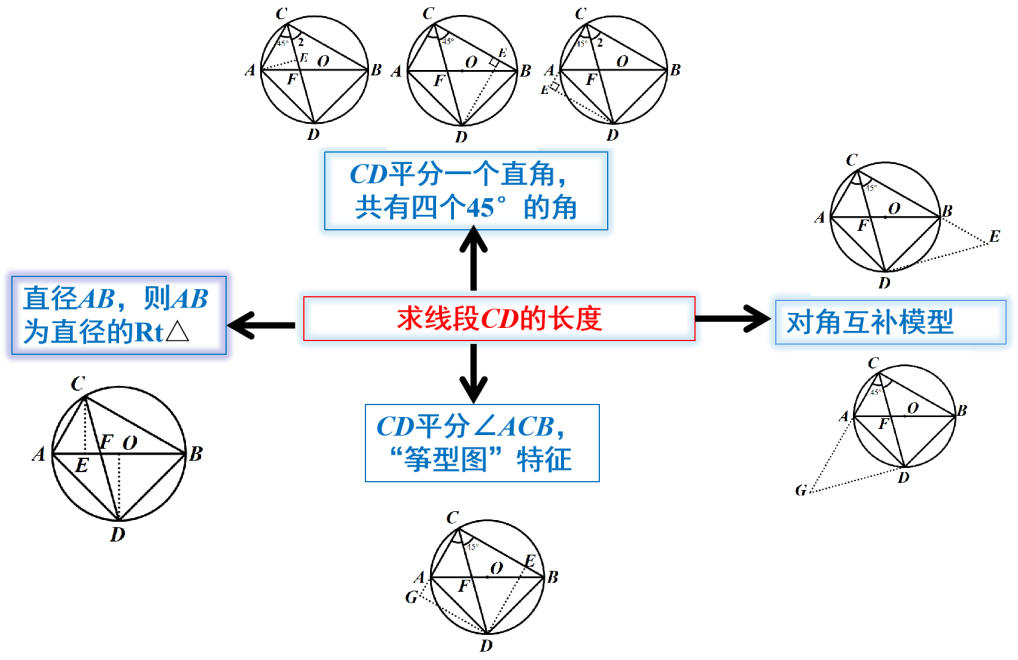
在第二次改编中，由于学生已经学习了全部的几何内容，内在一条件下，对同一问题的解决有了更多的思维出发点．圆外的边、角与圆内的边、角如何互化；圆的基本几何量与多边形的几何量如何进行互化结合；相关的“特征条件”除了可以作为全等三角形构造的切入点之外，还可以成为圆中相似三角形形及锐角三角函数的构造的切入点．在教学中我们不仅要教会学生本例题的求解方法，更重要的是引导学生感受和体会解题的思想与方法的自然生成过程，将前后所学进行面化和重组．

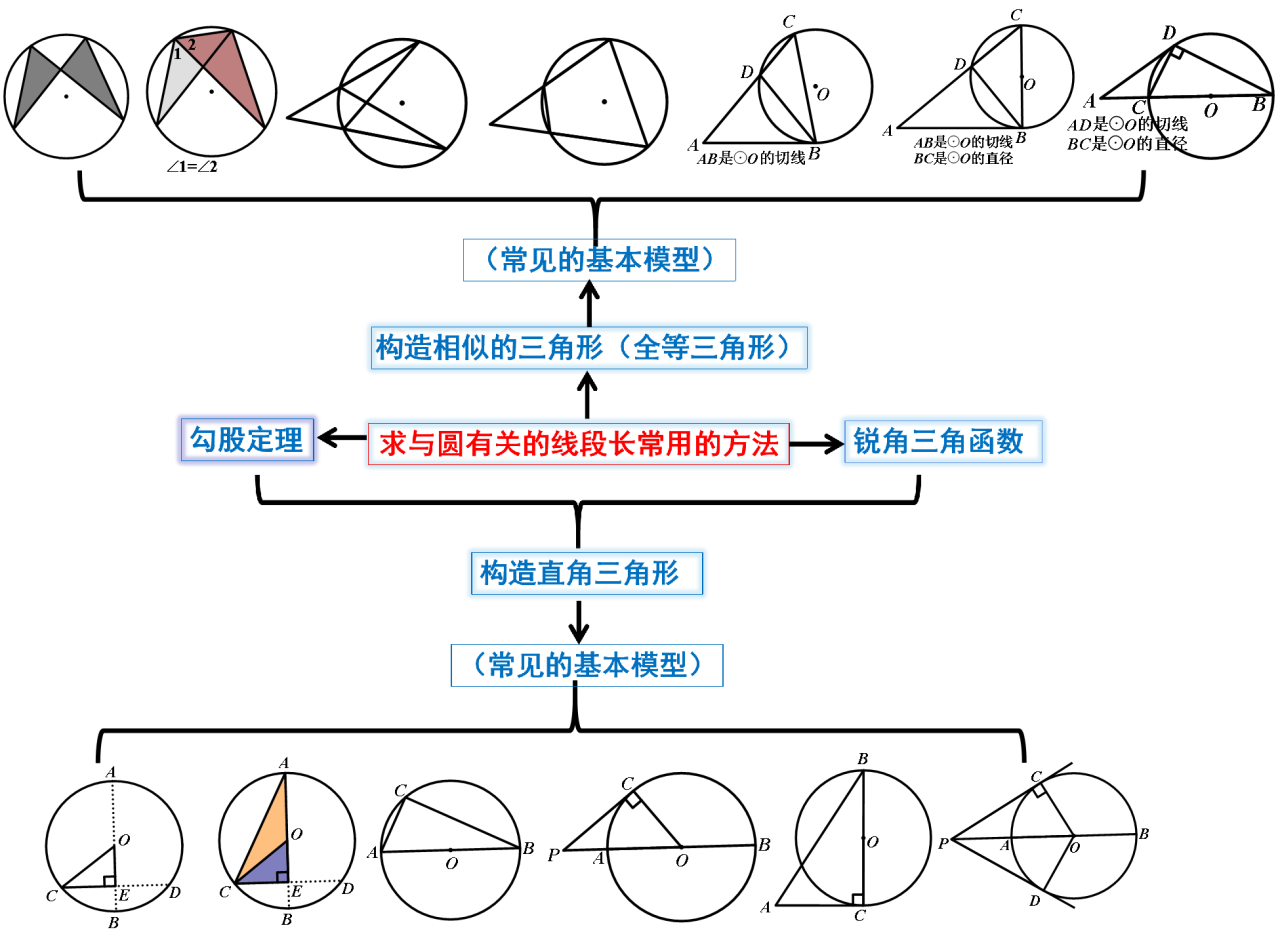
教师的教学难题是如何让学生体验解题方法的形成过程，从一道题“顿发的灵感”上升归纳为解一类题的思想方法的，而这些方法往往是多维度的、交错呈现的．借助思维导图图文并荗的直观性功能，不仅可以让学生清晰地体会到解题突破口的发现过程，而且可以一目了然地理解解题思想方法的挖掘 、使用过程，从而使学生正从会解一道题转变到会解一类题．甚至是如何解数学题． 例如本例题改编后的教学过程，事实上帮助学生汇总了“求与圆有关的线段长度的常用方法”．

结束语

总之，教师在教学中将课本例题讲透、讲活，在不同时期对例题的适度改编，在教学中进行深度剖析和变式探究，不仅巩固、加深已学过的新知识，还可兼顾新知与旧知的相互融合，引导学生发生新旧知的联系点，使得知识与方法在学生的脑海中呈现网状，那么在如此观念下进行教学，学生的收获不再只是单薄的，片面的，而是深度的具有综合性的．另外教材提供的例子虽然有限，但教材是教学的基本参考资料，是师生的思维间最为深刻的沟通媒介，是帮助学生形成探索学习方式、提升综合运用能力的大宝藏．教师应在学生已有的认知水平之上，基于不同的阶段的认知水平，不同的教学目标，进行不同程度的改编和教学设计，对其进行再创造，尽量借助例题的功能帮助学生实现知识结构的重组．

参考文献：

张振兴《一题多解，探寻教材例题的教学价值》 中国数学教育

张国汉《一道课本例题的再思考》 数学教学研究

陈 浮《立足课本，深挖细品》 福建中学数学

王天学《对一道课本例题的再设计》 中学数学杂志